트위터에서 구구단을 도해화한 사진이 화제가되고 있습니다. 트윗을 한 사람은 노벨상 수상자인 오무라 사토시 씨.. 가 아니고, 그의 친척인 오무라 켄이치 씨.
그는 아는 어머니로부터 초등학교 3 학년의 수학 프린트를 받아 보게 되었는데, 곱셈 구구단을 그림으로 그렸을 때의 아름다움에 감동을 해서 트윗을 했다고 하네요.

설이 길었는데요, 그럼 한번 구구단을 도해한 것이 어떤 것인지 한번 알아보도록 하겠습니다.
1단부터 9단까지 한 단 에 하나씩 동그란 원으로 나타내는 것인데요. 각각의 원에는 0부터 9까지의 눈금이 균등하게 적혀 있고, 0에서 시작해서 곱셈의 한자리 숫자를 차례로 선으로 연결합니다.
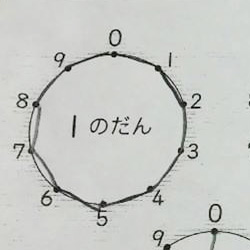
1단
예를 들어 1 단 이라면, 1X0 → 1X1 → 1X2 → 1X3 → 1X4... 이 되므로 아래와 같이 십각형이 완성됩니다.
9단
반대로 9단을 살펴보면, 한자리 수는 9X0=0 → 9X9=9 → 9X2=(1)8 → 9X3=(2)7... 이 되므로 1 단과 방향만 반대로 되어 완성된 모양은 1단과 같은 십각형이 됩니다. 1단과 9단에 이런 공통점이 있네요.

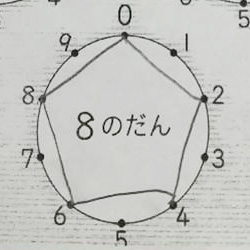
2단과 8단
2단은 0 → 2 → 4 → 6... 이 되므로 아래 사진 왼쪽의 오각형이 완성됩니다. 그런데 "8단"도 0 → 8 → 6 → 4 ...... 2 단 같은 오각형 됩니다. 역시 방향만 다르네요.

3단과 7단
3단과 7단도 같은 모양입니다. 그런데 이 두 단은 교차하는 지점이 많은 복잡한 형태가 완성됩니다. 나누어 떨어지지 않는 소수를 나타내는 듯 합니다.


4단과 6단
4단과 6단은 깔끔한 별 모양이 됩니다.


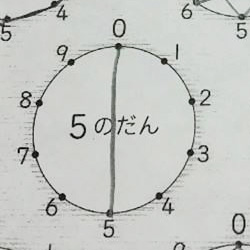
5단
유일하게 짝을 이루는 모양이 없는 것이 "5 단" 이었습니다. 5단의 답는 0과 5를 오갈 뿐이기 때문에 직선으로 나타납니다. 이렇게 단순해서 제일 외우기 쉬운지도 모르겠네요.
구구단을 처음 접했을때 느낌은.. 막연히 그냥 암기하는 것.. 이라는 느낌이었는데, 이렇게 도해화한 것을 보니 그 관계와 도형의 아름다움에 호기심이 생기는 듯 합니다.
이렇게 호기심이 생겨서, 수학을 일상서 친숙한 것으로 느껴지게 해 준다면, 이런 도해를 통해 구구단을 배워보는 것도 좋은 방법이라고, 그 시절의 필자에게 가르쳐주고 싶네요.